🚀线性表的定义和特点

🧨线性表的定义

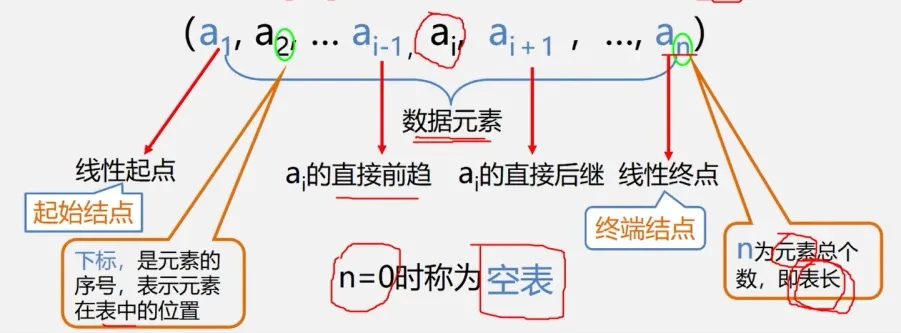
由n(n≥O)个数据特性相同的元素构成的有限序列称为线性表

🎊线性表的特点

• 线性表中元素的个数n(n≥O)定义为线性表的长度，n=O时称为空表

• 数据元素的个数n定义为表的长度

• 当n=0时称为空表

• 将非空的线性表(n>0)记作：(a₁, a₂, … an)

• 这里的数据元素ai(1≤i≤n)只是个抽象的符号，其具体含义在不同情况下可以不同。

• 在非空的线性表，有且仅有一个开始结点a1,它没有直接前趋，而仅有一个直接后继a2;

• 有且仅有一个终端结点an,它没有直接后继，而仅有一个直接前趋an-1;

• 其余的内部结点ai,(2<i<n-1)都有且仅有一个直接前趋ai-1和一个直接后继ai+1

🎨线性表的例子

26个英文字母组成的英文表：(A, B, C, …，Z)；学生信息表；学校历年电脑数量；12星座。

同一线性表中的元素必定具有相同的特性，数据元素之间关系是线性的。

线性表是一种典型的线性结构。

案例引入

案例1：

逻辑结构抽象为线性表存储结构

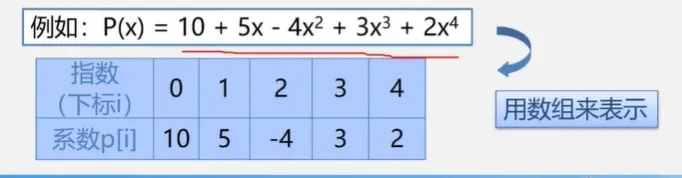
案例2：

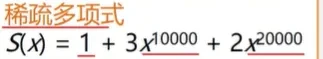
在处理这样的稀疏多项式时，就要用长度为20001的线性表来表示，而表中只有三个元素，将造成很大的存储空间浪费，因此我们可以改变元素设定，对多项式的每一项用(系数，指数)唯一确定。

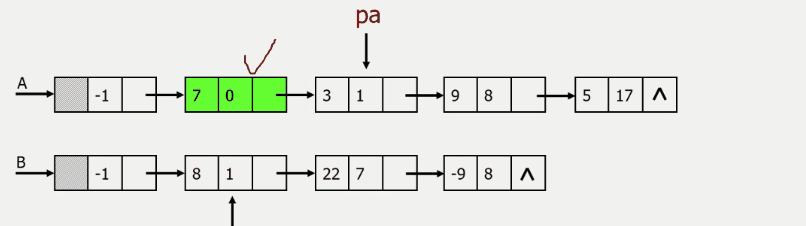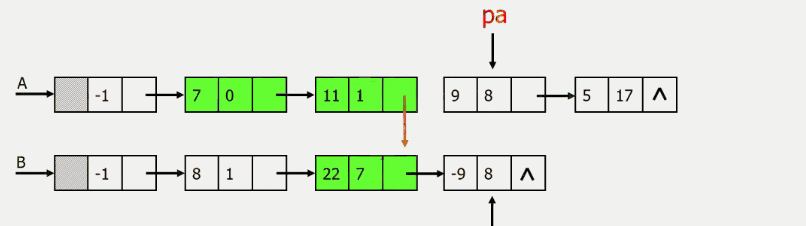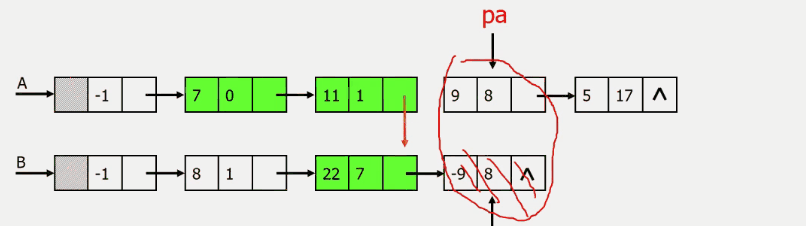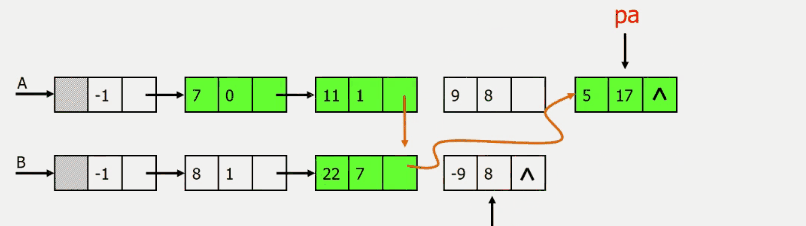
稀疏多项式的运算：

加法

A=((7,0),(3,1),(9,8),(5,17))[4项]

B=((8,1),(22,7),(-9,8),)[3项]

创建一个新的多项式c用来存放a与b和

分别从头遍历比较a和b的每一项

结果为((7,0),(11,1),(22,7),(5,17))

指数相同，对应系数相加，若其和不为零，则在c中增加一个新项

指数不相同，则将指数较小的项复制到c中

一个多项式已遍历完毕时，将另一个剩余项依次复制到c中即可

顺序存储结构存在问题

存储空间分配不灵活；

运算的空间复杂度高

尝试链式存储结构(不需要额外的空间只利用已有的空间)

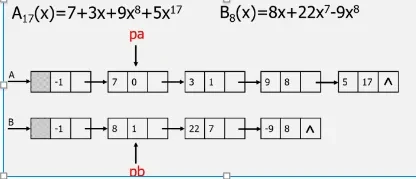
案例3：

图书表抽象为线性表

表中每本图书抽象线性表中数据元素

可以用顺序存储结构：

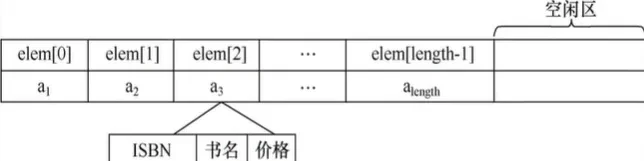
或链表

比较这两种存储结构的优缺点根据实际情况，选择适当的存储结构，实现此存储结构上的基本操作，利用基本操作完成功能。