🎍渐进时间复杂度

🎉渐进时间复杂度

若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n) = O(f(n)), 称O(f(n))为算法的渐进时间复杂度（O是数量级的符号），简称时间复杂度。

对于稍微复杂一些的算法，计算出算法中所有语句的频度通常是比较困难的。通常，算法的执行时间是随问题规模增长而增长的，因此对算法的评价通常只需考虑其随问题规模增长的趋势。

n -> ∞时，T(n) / n³ -> 2,这表示n充分大时 ，T(n)于n³是同阶或同数量级，引入大“O”记号，则T（n）可记作：

T(n) = O(n³)

这就是求解矩阵相乘问题的算法的渐进时间复杂度

一般情况下，不必计算所有操作的执行次数，而值考虑算法中基本操作执行次数，它是问题规模n的某个函数，用T（n）表示。

算法中基本语句重复执行的次数是问题规模n的某个函数f(n)，算法的时间量度记作：T(n) = O(f(n))

• 基本语句：

1. 算法中重复执行次数和算法的执行时间成正比的语句；
2. 对算法运行的时间贡献最大；
3. 执行次数最多。

• 问题规模n：

n越大算法的执行时间越长

1. 排序：n为记录数
2. 矩阵：n为矩阵的阶数
3. 多项式：n为多项式的项数
4. 集合：n为元素个数
5. 树：n为树的结点个数
6. 图：n为图的顶点数或边数

🎎分析算法时间复杂度的基本方法

1. 找出语句频度最大的那条语句作为基本语句

2. 计算基本语句的频度得到问题规模n的某个函数f(n)

3. 取其数量级用符号"O"表示

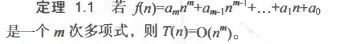
举例1：

x = 0; y = 0;															//执行一次
for (int k = 0; k < n; k ++ )							//外层语句判断 n + 1次
	x ++;																		//循环体执行n次
for (int i = 0; i < n; i ++ )							//外层语句判断 n + 1次
	for (int j = 0; j < n; j ++ )						//循环体内的外层判断语句n+1次 循环体n次所以是n(n+1)次
  	y ++;																	//循环体内为n*n

通常循环体嵌套最深的往往是执行次数最多的

所以该例的时间复杂度为

T(n) = O(n²)

忽略所有低次幂项和最高次幂的系数，这样可以简化算法分析，也体现出了增长率的含义。

时间复杂度是由嵌套最深层语句的频度决定的。

举例2：

举例3：

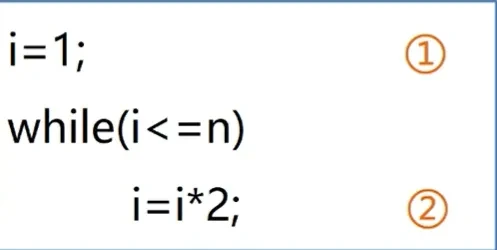
🎃常数阶

for (i = 0; i < 1000; i ++) {
	x ++;
  s = 0;
}

实际上，如果算法的执行时间不随问题规模n的增加而增长，算法中语句频度就是某个常数。即使这个常数再大，算法的时间复杂度都是O(1)。

🎉线性阶

给小灰一个长度为10cm的面包，小灰每三分钟吃掉1cm，那么他吃掉整个面包要多久？

答案自然是3*10=30min

如果面包的长度为n cm呢？

此时吃掉整个面包需要3*n即3n分钟。

如果用一个函数来表达吃掉整个面包所需要的时间可以记作T(n)=3n

(n表示面包的长度即处理的数据的规模)

🎐对数阶

给小灰一个长度为16cm的面包，小灰小灰每5min吃掉面包剩余长度的一半，第1min吃掉8cm，第2min吃掉4cm，第三min吃掉2cm…那么小灰把面包吃得只剩下1cm，需要多少天呢？

这个问题翻译一下，就是数字16不断地除以2，除几次以后的结果等于1？

这里要涉及到数学当中的对数，以2位底，16的对数，可以简写为log₂16。

因此，把面包吃得只剩下1寸，需要 5*log₂16=5*4=20 min

如果面包的长度为n cm呢？

此时吃掉整个面包需要5*log₂n分钟记作T(n)=5*log₂n

🎎平方阶

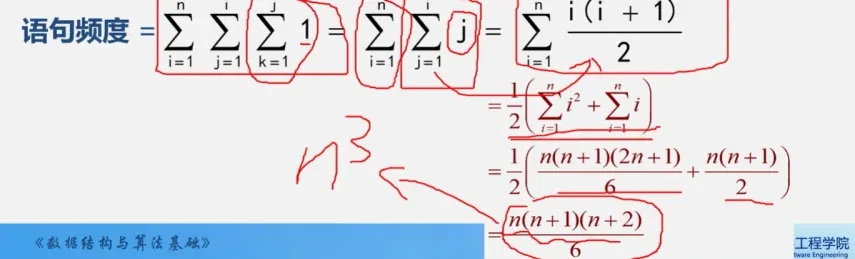
由于当i=0时内循环执行n次，当i=1时内循环执行n-1次，…，当i=n-1时内循环执行1次总执行次数

n+(n-1)++(n-2)+…+1=n(n+1)/2

时间复杂度是O(n²)

🥽立方阶

🧶最好、最坏和平均时间复杂度

有的情况算法的基本操作重复执行的次数还随问题输入的数据集不同而不同

通常考虑最坏和平均

但有时平均比较难计算

只考虑最坏时间复杂度，最坏情况运行时间是一种保证，那就是运行时间不会再坏了

🎑计算公式

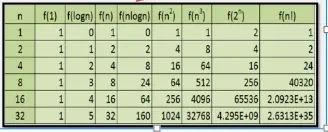
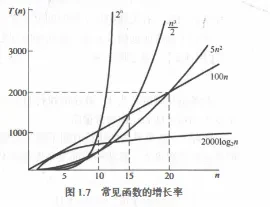
常见的时间复杂度按数量级递增排列依次为：

• 常数阶O(1)
• 对数阶O(log₂n)
• 线性阶O(n)
• 线性对数阶O(nlog₂n)
• 平方阶O(n²)
• 立方阶O(n³)
• …
• k次方阶O(n k次方)
• 指数阶O(2 n次方)

🎉算法的空间复杂度

算法本身要占据的空间：输入/输出、指令、常数、变量等

算法要使用的辅助空间

若输入数据所占据的空间只取决于问题本身和算法无关，这样只需分析该算法在实现时所需的辅助单元即可，若算法执行时所需的辅助单元相对于输入数据量而言是个常数，则称此算法为原地施工，空间复杂度为O(1)

绝大多数情况下，时间复杂度更重要一些，我们宁愿多分配一些内存空间也要提升程序的执行速度。